【数学科 柴田 孝人】
1.新入試問題はどのようなものか
2020年度の大学入試改革での大学入学テスト(新テスト)は,「思考力・判断力・表現力を問う」方針のもと現在の高1から始まります。今までは,指導要領が変わると数学は単純に単元が少し入れ替わる程度でしたが,今回の改革は全く異なるものです。
数学は、マークシート式の問題とともに,「数学Ⅰ」「数学Ⅰ・数学A」受検者を対象に、「数学Ⅰ」の範囲から3問程度記述式の問題が出題され,試験時間は現行の60分から70分程度に延長される予定です。また,マークシート式問題も選択肢の中から正解を選択する場合,答えが複数あったり,また,内容も思考力を問う問題に変わる。ということが現時点で決まっていることです。
文部科学省は2017年11月に全国の学校で「大学入学共通テスト」の試行調査(プレテスト)の問題と結果を公表しました。数学I・Aは身近なテーマについての場面などを多く設定し、ページ数が2倍になり,数学Ⅱ・Bと合わせると8割増。複数の文章や図、グラフを読ませる問題が多くなりました。以下に出題された問題例を提示します。
数Ⅱ・B数列の問題の例

解答
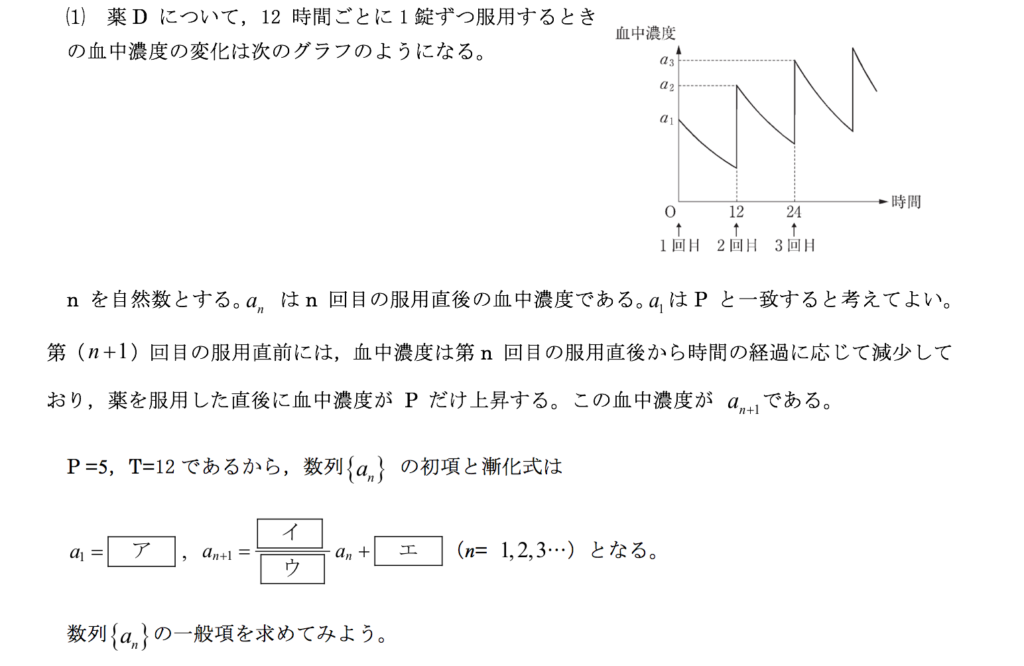

この問題を見ると,さながらどこかの私大の獣医学部か薬学部の入試問題のようです…。また,このときのマークシート式の正答率は非常に低いもので,数学I・Aの記述式問題3問の正答率はいずれも10%未満でした。
2.これからの数学の勉強のしかた
今まではセンター試験の数学では、解法パターンをただ暗記したり、誘導を頼りに解いていくという勉強法でもなんとかなっていたかもしれません。しかし、これからは上記の例を見ても、それが通用しなくなることは明かです。では、新テストの問題に対応する力をつけるためには、どのようにすればいいのでしょうか?
実は、この問題を解く力をつけるにはまさに数学としての王道の勉強をするしかないのです。すなわち、
①「教科書などの導入部分や定義の説明をきちんと読み理解すること」
例えば、公式一つ一つについても、ただ、暗記して使うのではなく、なぜそのような公式が導き出せるのか,考え方を理解して自分でもできるようにすることが要求されます。
②「多角的に問題を解くことができるように水平的な解法を訓練すること」
上記の例でも2通りの漸化式の解き方が問われているように、問題を解くとき、1つの単元の問題としてだけではなく、別の単元からのアプローチができないかを考えることが重要です。「別解がある」というのは数学の面白さの一つではあるのですが、このような多角的な問題の解き方が新入試問題で本格的に問われることになりそうです。これには、垂直的な単元理解と並行して、分野を跨いだ水平的な解法訓練が必要です。
以上、新入試問題に向けた総論を述べましたが、主体的・対話的で深い学び方として、学校ではアクティブラーニングが昨今積極的に取り入れられているものと思います。例えば数学については、いろいろな解法を考えて意見を言い合うのも面白いかもしれません。いすれにしても,受け身になっていてはいい結果は望めませんので,前向きに考えてどんどん自分の考え・知識を醸成していくことが重要です。
著者プロフィール
札幌白石高校卒、北海道大学水産学部卒。大手学習塾、予備校にて20年以上に渡り、個人指導から講座授業まで幅広く受験指導を行っている。特に教材研究・開発には余念がなく、「柴田文庫」と呼ばれるほどに、受験数学に関するあらゆる参考書を日々研究している。現在、当校数学科教員。
